You are here
Taking on the Great Mathematical Conjectures
There are hundreds of them, covering all fields of mathematics, and the most impenetrable are often based on the simplest of propositions. Mathematicians call them “conjectures”: theorems or hypotheses that have a strong probability of being correct, but that no one has ever managed to prove or refute. Mathematicians agree that it takes as much imagination – along with a wealth of fresh ideas – to solve these puzzles as to devise them. But what exactly are they about? What role do conjectures play in mathematics? And what are the concrete benefits of research in this strange but fascinating field?
The history of the discipline is strewn with emblematic conjectures. “I have a truly marvellous demonstration of this proposition, which this margin is too narrow to contain,” wrote Pierre de Fermat in the 17th century as an annotation in a book.1 Fermat’s Last Theorem (that no three positive integers x, y and z exist such as xn+yn=zn, where n is an integer greater than 2) was not verified until 1994, by the British mathematician Andrew Wiles. Whether or not Fermat himself had managed to support his theory, he was convinced that a result could be true even though he was not able to substantiate it. “The demonstration of a mathematical theorem, in other words its proof, is a logical sequence that relies on a system of deduction,” says Martin Andler, professor emeritus at the LMV.2 “Yet devising a demonstration, let alone formulating a conjecture, takes real imagination. The way certain mathematicians have done so is like taking a leap into the void.”

Over the decades, the idea of “conjecture” has been designated by various terms, including that of “hypothesis”. For a mathematician, its public announcement is a major undertaking and a commitment, a decision to put an issue in the spotlight and encourage others to mull it over. Therefore, such an assumption must have substance, be of interest and lead to something. But what makes a theoretician believe that an unproven proposition is true? There are three main factors: analogy, experimentation and intuition. Analogy consists in identifying similarities between two problems and applying what works for one to the other. Alternatively, a mathematician can conduct trials or experiments that yield new ideas. And today, calculations performed by computer can be used to validate an intuitive insight.

Does this mean that such assumptions are beyond the grasp of non-mathematicians? Although their resolution has in some cases taken hundreds of years, certain propositions can be easily understood. One example is the Syracuse Conjecture, named after the American university where the problem originally posed by Lothar Collatz was introduced in the 1930s. The Collatz sequence, later called the Syracuse sequence, is a series of natural numbers defined as follows:
Start with a whole number greater than 1. If it is odd, multiply it by 3 and add 1. If it is even, divide it by 2. Repeating this operation indefinitely means obtaining a sequence of positive integers, each of which depends only on its predecessor. For example, 5 (odd) multiplied by 3 plus 1 equals 16 (even). Then 16 divided by 2 is 8, then 4, then 2, then 1, then again 4, 2, 1, etc. To this day, no mathematician has identified any number, however large, that does not lead to the sequence 4, 2, 1. The Syracuse Conjecture states that the sequence of any positive whole number will eventually reach 1. But is this true for all starting numbers? That is the question that mathematicians seek to answer in order to confirm this thesis.
Peaks to be scaled together
“In the mountain range of mathematics, conjectures are the peaks to be climbed. But getting there means having to work one’s way up and learning all there is to know about everything along the way,” explains Emmanuel Royer, deputy scientific director of the CNRS National Institute for Mathematical Sciences and their Interactions (INSMI).
In a way, conjectures are the “lighthouses” that guide mathematicians – like Fermat’s Theorem, demonstrated by Wiles more than 300 years after the French scientist jotted down his legendary note. “When the theorem was verified, some researchers were disappointed because it marked the end of a powerful driver for the formulation of mathematical theories,” Andler recounts. Certain conjectures last for centuries, resisting the combined efforts of generations of great minds. The search for solutions becomes a huge collective endeavour, an intellectual relay race run over decades and centuries. Only one mathematician can reach the “finish line”, nonetheless carrying the baton handed down by their predecessors.
Beyond their use in mathematics, the results can seem disconnected from any concrete application. However, the negative response formulated in the 1930s by Alan Turing and Alonzo Church to one of the 20th century’s 23 problemsFermerThe 23 Problems for the 20th Century, also called Hilbert’s Problems, were questions that remained unsolved as of 1900 and that the German mathematician David Hilbert considered to be of key importance for the century that had just begun. Most have been demonstrated today, but five are still the subject of research., the decision (“Entscheidung”) problem proposed by the German mathematician David Hilbert in 1900, proved to be crucial in laying the theoretical foundations of computer science. And Fermat’s Theorem, which belongs to the mathematical field of number theory, led to the development of the most effective modern-day cryptography methods.



What becomes of a conjecture? It can be proven true or false, but that’s not the only possible outcome. In 1931, the young Austrian-born logician Kurt Gödel demonstrated that there are undecidable statements that can be neither confirmed nor disproved, thus marking a turning point in the history of logic. Other assumptions reach a happy – although belated – ending, like the one proposed by Poincaré.
Poincaré, from conjecture to theorem
In 1904, the French scientist Henri Poincaré proposed a characterisation of the sphere in three dimensions. “This followed some 20 failed demonstrations by other mathematicians, half of whom claiming it was true and the other half it was false,” reports Gérard Besson, a mathematician at the Institut Fourier.3 A real breakthrough didn’t come until 1982, when the American mathematician William Thurston made Poincaré’s question part of a wider conjecture. By explaining how all three-dimensional geometric objects – and not just the sphere – should be, he opened a path that sped up the race towards a resolution. By introducing a new method, his fellow US scientist Richard Hamilton contributed an important step forward in 1983. Ultimately, it was the Russian mathematician Grigori Perelman who, in 2003, announced that he had reached the final step.
He spent seven years drafting a demonstration filled with ellipses and very difficult to grasp for his peer reviewers. At least four groups (one based in China, two in the United States and a French-Spanish team that included Besson) set out to verify his work, a process that lasted another seven years. “It was great to think that we were going to be able to understand the methods for solving the famous Poincaré Conjecture,” the researcher recalls. “At certain points we doubted the solution proposed by Perelman, but he had identified all the pitfalls. I quite admire what he did.”
The Russian mathematician refused to accept the Fields Medal 2010, as well as the $1 million prize awarded by the Clay Institute for solving one of the “seven millennium problemsFermerAt the Collège de France in 2000, the Clay Mathematics Institute presented seven major mathematical problems that pose a challenge to the scientific community. Endowed with a prize of $1 million each, these problems include the Poincaré Conjecture – demonstrated since by Perelman –, as well as the question based on the Navier-Stokes equations.”, and withdrew from the mathematics community. Nonetheless, his prize served to fund a chair at the Institut Henri Poincaré, in Paris. “Its goal is to offer promising young researchers an opportunity to work for six months in a mathematical environment of excellence,” explains the institute’s director Sylvie Benzoni.4 With two laureates per year, these scholarships finance projects by young mathematicians specialising in various fields, ranging from geometry to probability and the study of dynamic systems. While Perelman’s result has not had an impact beyond mathematics, the method proposed by Hamilton found an application in the denoising of digital images (the elimination of unwanted information or other damage to the image). Today, mathematicians are examining closed objects in dimension 4, a category that could be used to characterise the Universe.
The Riemann hypothesis impervious to all attempts
“In number theory, it’s often not the last step that’s missing, but the first,” notes Gérald Tenenbaum, professor emeritus at the Université de Lorraine (northeastern France). “In the case of the Riemann hypothesis, there are some approaches based on analogies, but no real strategy has emerged.” The conjecture, which dates back to 1859, focuses on primes – numbers that have the property of being divisible only by themselves and by 1, like 13. The goal is to describe how these numbers are distributed among all integers. To solve the problem, the German mathematician Riemann used the definition of the “zeta function”, which had already been considered by the Swiss scientist Euler in the 18th century, and showed that it made it possible to describe the frequency of occurrences of prime numbers with great precision.
But not everyone agreed with this theory. “A number of research studies use the hypothesis as a starting point, which means that the results obtained are conditional,” Tenenbaum explains. “The conjecture leads to many remarkable consequences, only one of which needs to be disproven in order to refute it.” If the assumption were to be proven false, a great many conditional theorems would have no more basis. Still, even if it is refuted, the thesis indisputably yields an image that is very close to reality: so far more than 10 billion values have been verified by computer and corroborate the hypothesis. However, for the mathematical community, this is evidence but not proof!
IT to the rescue?
Will the confirmation or rejection of conjectures be facilitated by the emerging field of computer-assisted proof? Digital tools like the French Coq system5 can be used to write and verify proofs, providing correction guarantees in fields where evidence becomes complex. They showed their effectiveness in 2010 with the four colour theorem, a hypothesis that had spawned many false demonstrations. The theorem asserts that it is possible, using only four different colours, to divide any map into contiguous regions so that any two adjacent zones always have a different shade. These tools led to the acceptance of one demonstration, announced in 1976 and based on mathematical arguments backed by several thousand cases calculated for the first time by computer. The problem of demonstrating the theorem then became one of validation: first of the exploration algorithm, and then of its implementation in the form of a program. “The challenge of verifying a theorem by computer involves checking the logical mathematical reasoning as well as the calculations, in order to ensure that they follow the laws of logic,” says Christine Paulin-Mohring, a researcher at the Laboratory for Computer Science (LRI).6
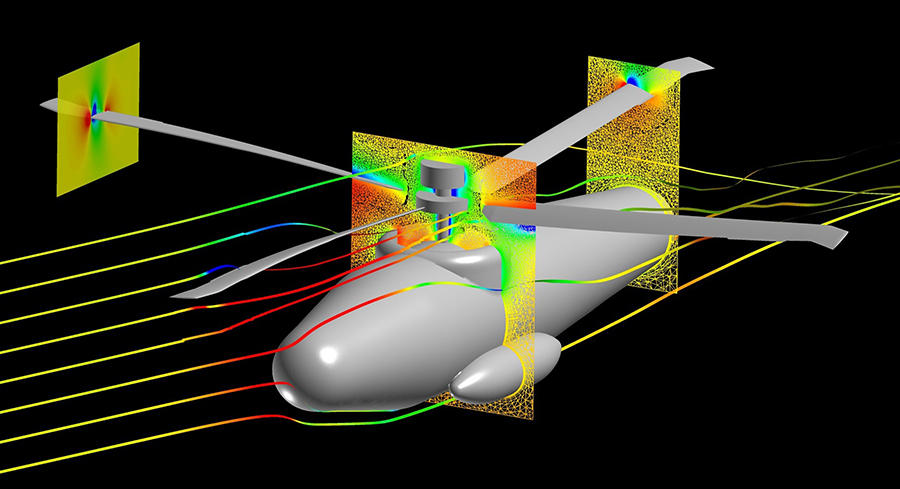
The Navier-Stokes equations, an open question
In addition to conjectures, the field of mathematics also draws impetus from open questions, like those concerning the Navier-Stokes equations, established in the 19th century, which form the basis of one of the “millennium problems”. Their main purpose is to describe the movement of fluids – including water, air or viscous liquids like oil –, which requires knowing their speed at any point in space. These are therefore differential equations, with an unknown range of speed, also known as “nonlinear” equations: the conditions vary depending on the fluid being studied, which may be subject to turbulence (like an airplane moving through the air). “There are so many interesting issues related to this subject that one can spend a lot of time on it without solving the central question,” observes Isabelle Gallagher, a mathematician at the Department of Mathematics and Applications of the ENS.7
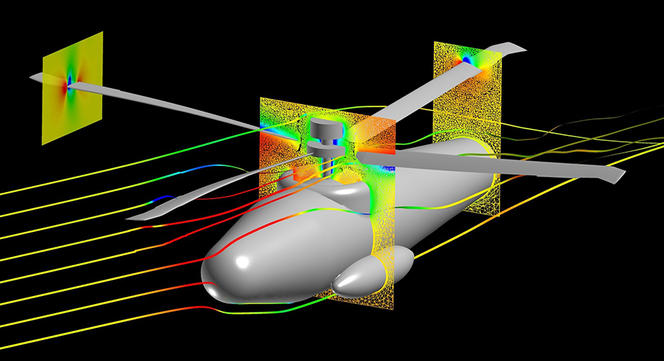
“In addition, it’s impossible to elucidate directly – it has to be approached from other angles.” Nonetheless, the Navier-Stokes equations are widely used for modelling meteorological phenomena and studying ocean currents, as well as in aerodynamics. The essential difference between a conjecture and an open question is that the former calls for a precise solution, whereas there is greater uncertainty for the latter. An answer could open novel paths that may eventually lead to a new hypothesis. And the reason why solving a conjecture is such a fascinating experience is that once the mathematicians have reached their goal, they can look back at the length and breadth of their journey, and move on to the next adventure.
__________________________________________
France’s Year of Mathematics 2019-2020
Launched in October 2019 as one of the events surrounding the 80th anniversary of the CNRS, in partnership with the French Ministry of National Education and Youth, the Year of Mathematics conveys several messages: that maths is a living science, ever present in society; that studying it can lead to multiple professional opportunities; that teaching it must be made once again a desirable profession; that this discipline is not reserved for boys. Through its National Institute for Mathematical Sciences and their Interactions (INSMI), the CNRS is active in promoting mathematics education. It participates in programmes aimed at secondary school teachers and is involved in the organisation of public events.
To find out more: http://annee.math.cnrs.fr
- 1. Handwritten note in Arithmetica by Diophantus of Alexandria (3rd century AD).
- 2. Laboratoire de Mathématiques de Versailles (CNRS / Université de Versailles Saint-Quentin-en-Yvelines).
- 3. CNRS / Université Grenoble-Alpes.
- 4. CNRS / Sorbonne Université.
- 5. Coq: a proof assistant developed by the INRIA at the Proofs, Programs and Systems laboratory, now part of the Research Institute on the Foundations of Computer Science, (IRIF – CNRS / Université de Paris).
- 6. CNRS / Université Paris-Saclay.
- 7. CNRS / ENS Paris.
Explore more
Author
After a degree in environmental studies at Paul Sabatier University in Toulouse, then in science journalism at Paris-Diderot University in Paris, Anaïs Culot worked in media relations at the CNRS and now collaborates with various magazines, including CNRS Le Journal, I'MTech and Science & Vie.