What Makes the Earth’s Mantle Flow?

07.20.2016, by

Artist’s view of the Earth’s interior showing, under the crust, the mantle’s movements responsible for plate tectonics.

By analyzing microscopic defects in the mineral that makes up 60% of the Earth’s mantle, researchers have uncovered what makes this solid rock flow.

“Humans have walked on the Moon. Robots survey the surface of Mars. Probes have been sent out to the outer limits of the Solar System. Yet there is still no way for us to get inside our own planet,” points out Patrick Cordier, a professor at the Université de Lille 1 and researcher at the UMET1 laboratory. He recently presented, along with his team, the results of four years of research carried out as part of the RheoMan project to model the rheology (deformation and flow) of the Earth’s mantle. Awarded an Advanced Grant funded by the European Research Council, this 5-year project hones in on the character and behavior of mantle rock by translating them into equations and running computer simulations.

Modeling the depths of the Earth

Wedged between the Earth’s crust and its core, the mantle is exposed to searing temperatures of up to several thousand degrees and pressure that is one million times higher than atmospheric pressure. Geological activity on the Earth’s surface is a result of deep convection movements, which stir the mantle as far as 3000 kilometers below our feet. At such depths and in such extreme conditions, studying and understanding the continual flow of solid mantle rocks is a real scientific challenge. But even if the mantle remains largely inaccessible, its dynamics are slowly being unearthed.

As direct observation is impossible, we had to start from the known laws that govern matter.

What we need to bear in mind is that despite being classified as solid on the geological timescale, mantle rock is deformed on an ongoing basis. This capacity for deformation is assessed in terms of viscosity, measured in pascal-seconds (Pa. s), which corresponds to a material’s resistance to flow. While liquid water has a viscosity of 10^-3 Pa. s, honey of 10 Pa. s and bitumen of 108 Pa. s, that of mantle material varies between 10¹⁸ and 10²¹ Pa. s. This level of viscosity means that the mantle moves at a speed of several centimeters per year.

It is on a microscopic scale inside mantle material that the Earth’s major deformations are played out. “As direct observation is impossible, we had to start from the known laws that govern matter—using suitably robust theoretical concepts and powerful-enough computers to obtain results,” explains the researcher who was awarded, in December 2015, the Dana Medal by the Mineralogical Society of America. “A major challenge lies in finding the means to perform experiments in increasingly extreme conditions, in terms of temperature and pressure. Calculations let us override such experimental limitations.” To get around the fact that direct analysis of rock properties in the mantle was impossible, Cordier’s team was able to develop multi-scale numerical models, which reflect their behavior. Three levels of models—atomic, microscopic and macroscopic—were combined in their analysis.

Solving the olivine paradox

Using this approach, the team was able to tackle a longstanding mystery surrounding the deformation of olivine, a mineral that makes up to 60% of the upper mantle.

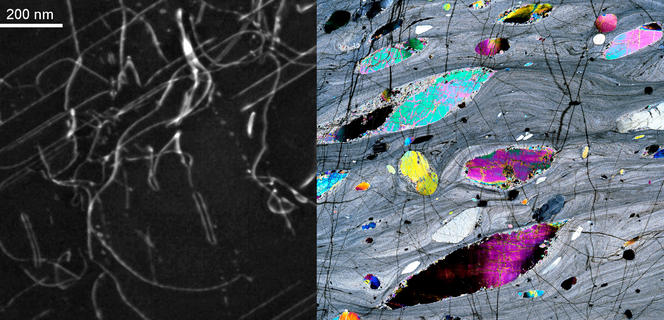
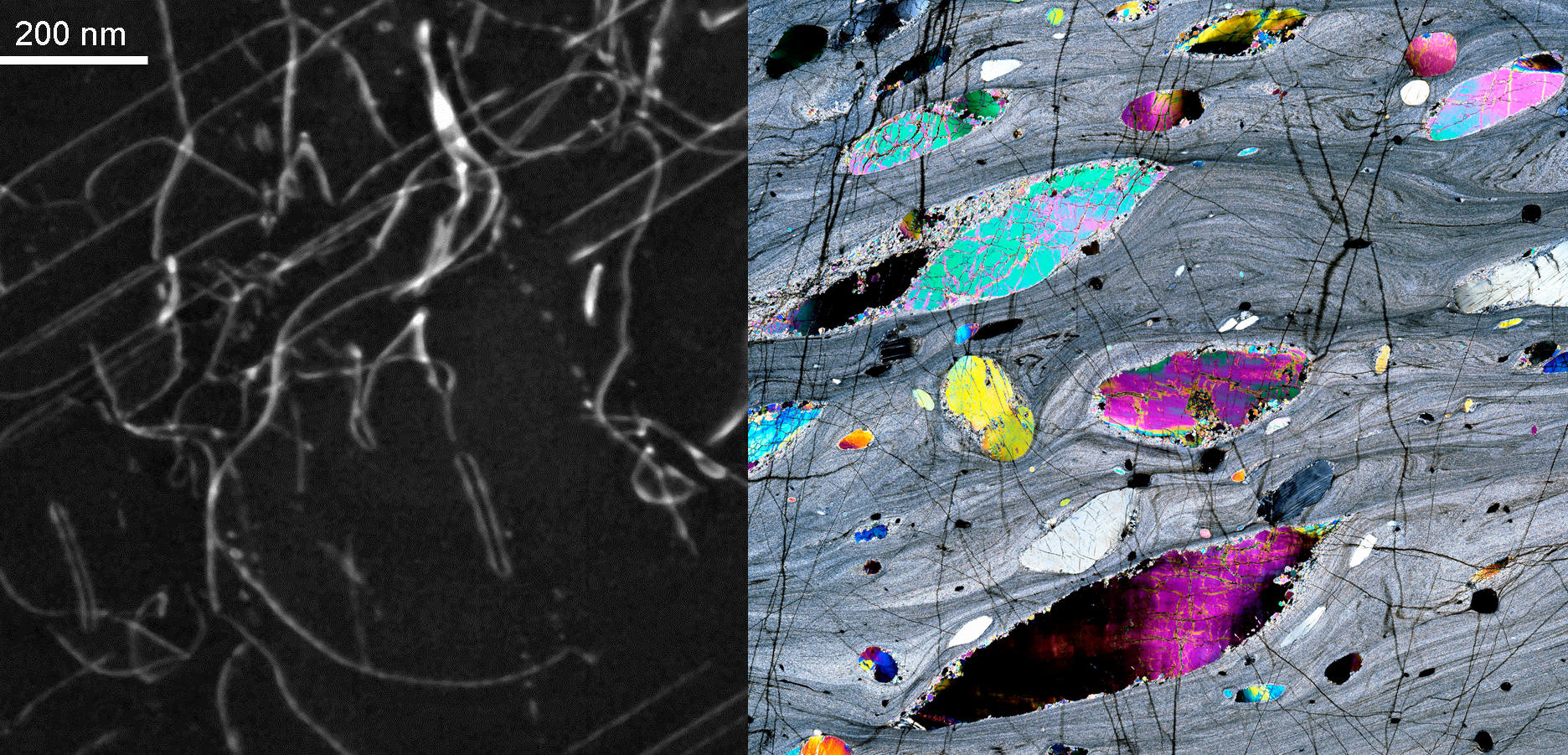
©S. Demouchy-P. Cordier / D. Wiersma / SPL / Cosmos

Left, olivine crystal deformed by pressure, with dislocations visible under an electron microscope. Right, deformed olivine crystals seen under polarized light.

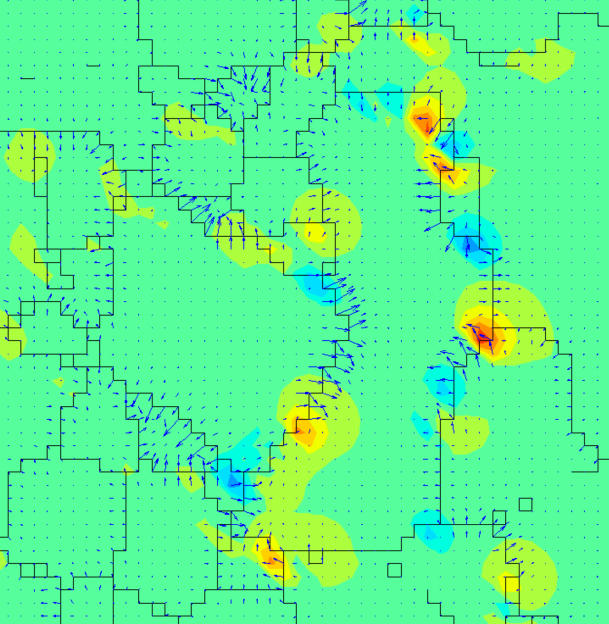
To put things simply, we can see rock as a cluster of mineral grains. Any rock deformation results from a modification, either in the atomic structure of the grains making up the rock, or in the boundary between these grains. The geologists started off by identifying the crystal defects in olivine. “Without crystal defects, we would live in an incredibly hard world where metallurgy would be impossible, where the only metals would be brittle ones. Crystal defects endow materials with a capacity to be shaped, deformed or forged,” explains Cordier. “What we had to find out, regarding olivine in a 3D space, was how it was able to make shear movements in all directions.”

Until now, scientists only knew of one type of olivine defect causing deformation: dislocations (line defects in the crystal structure). The latter, however, fail to account for translation (sliding movement) in some directions. With the help of electron microscopy—which lets us probe olivine’s atomic structure—Cordier and his colleagues have succeeded in showing the existence of disclinations (or defects linked to crystal rotations). These defects now offer an explanation for the rotation movements observed in the boundaries of mantle rock.

On this map representing the interfaces between grains (grain boundaries) as black lines, disclinations identified by electron microscopy appear as red and blue blotches.

This research makes significant headway in materials science and helps deepen our understanding of the plasticity of the Earth’s mantle rock. Disclinations stand out as a new concept which researchers can use to explain a number of phenomena related to the mechanics of solid rock—namely when it is out of physical reach. This Earth model could be used for studying rocky exoplanets, for example.

Footnotes