You are here
Cryptography faces the threat of quantum technology

How did a mathematician like you come to design secret codes?
Benjamin Wesolowski1: As far back as I can remember, I have always liked mathematics. I indulged in this passion, which led me to the Federal Institute of Technology (EPFL) in Lausanne (Switzerland), where I completed my bachelor’s and master’s degrees, and then my PhD. That’s where I really discovered cryptology, a discipline that immediately won over the math enthusiast that I was, and still am! But this story probably began much earlier, for as a child I loved spy games in magazines that involved decoding a coded text.
Your career path earnt you a 2023 ERC Starting Grant. What exactly is it?
B. W.: The ERC Starting Grant is awarded by the European Research Council to fund young researchers. In my case, the project in question aims to solidify lattice-based and isogeny-based cryptography. My goal is to employ existing mathematical theories that have been little-used in the field. These tools can provide a fresh perspective in the discipline, and can also help develop new and rigorous foundations, notably to estimate the complexity of problems.
Cryptography experienced significant progress in the 1970s when cryptographers began to draw on hitherto untapped mathematical theories, such as number theory. This major advance was public-key cryptography. Today the discipline faces new challenges, in particular from quantum computers. Problems are becoming more and more complex, and mathematical exploration is playing an increasingly important role.
What is the difference between public-key cryptography and secret-key cryptography?
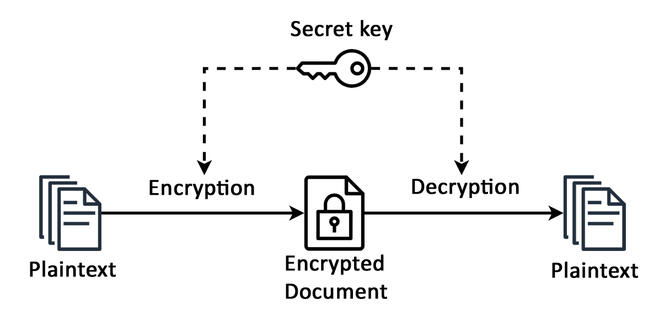
B. W.: Secret-key cryptography is the older method. The idea is simple: two people want to communicate secretly on an insecure channel (their messages can be intercepted). They agree on an encryption procedure, transforming a message into an unintelligible text, which is sent via the channel, and then decoded by the recipient. To ensure that only the latter can decrypt the data, the partners agree in advance on a secret ingredient that enables encryption and decryption – the secret key. Without it, a spy cannot read the intercepted information.
Public-key cryptography responds to the following question: how can the interlocutors choose such a secret key without having to physically meet, given that all of their communications can be intercepted? It is a problem that was long thought unsolvable, until public-key cryptography came to light.
How does it work? Why is it so widely used today for communications security?
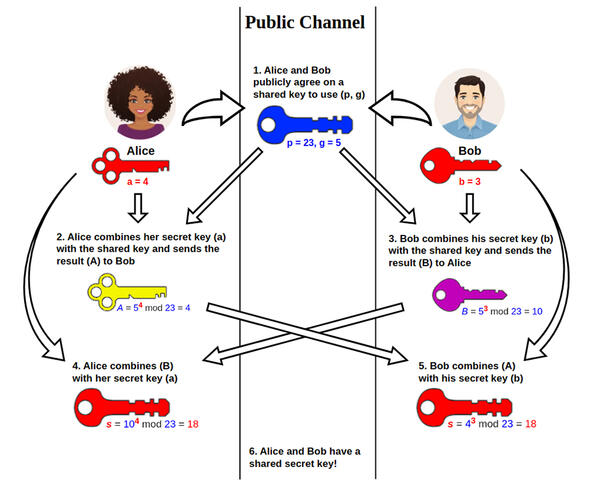
B. W.: The Diffie-Hellman protocol, which was the first in the field and is still widely used today, is quite simple. The contacts begin by agreeing on a ‘number’ n, which is not a secret. The first person secretly chooses a whole number x, and sends nx. The second also confidentially selects a whole number, and sends ny. Each of them can calculate nxy. The first knows x (their own secret) and ny (which they have received), and can therefore guess (ny)x. Similarly, the second can work out (nx)y. A spy may have intercepted n, nx and ny, but the ‘number’ nxy never transited on the insecure channel. It is a secret shared by the two partners, who can henceforth use it as a secret key.
In actual fact, a spy who sees nx could try to figure out x; this is what is known as a logarithm. Should they succeed in doing so, they can then determine (ny)x, and everything crumbles. Calculating logarithms for usual numbers is easy, but n can be chosen from other types of ‘numbers’ in which this problem is much more complex. This is what is known as a discrete logarithm problem.
Multiple methods have been developed to solve it, much more efficiently than a simple exhaustive search. However, they require enormous computing power when the numbers in question are very large. This means that with sufficiently large parameters, even running all of the world’s computers for billions of years would not be enough to solve the problem. This is why the discrete logarithm problem is considered difficult, and the Diffie-Hellman protocol secure in protecting our communications.
This applies to classical computers. What about quantum computers?
B. W.: That’s something very different altogether! Supposing an individual has access to a sufficiently stable quantum computer, they could effectively solve the discrete logarithm problem, thereby breaking numerous cryptography protocols. However, this does not mean that a quantum computer is just a super classical computer, only more powerful. Simply put, it functions differently: instead of classical bits, it is based on quantum bits, which can encode a superposition of multiple different states. This property represents an advantage that can prove considerable for quantum computers in solving a limited number of problems. The discrete logarithm is precisely one for which the quantum computer would be much more effective!
Should we be worried about the security of our communications?
B. W.: Not at this stage, for quantum computers remain theoretical for now. The existing prototypes cannot break today’s cryptography methods.
But what will happen if a sufficiently large and stable quantum computer is created?
B. W.: It would be better not to wait for the threat to materialise to ask the question! If we have to change all of our communication standards, it will take years. In addition, one can easily imagine individuals or intelligence agencies carefully recording current encrypted exchanges. They may not be able to read them today, but it will turn into a mine of information the day they have access to a quantum computer. It is an attack known as ‘harvest now, decrypt later’. This has already occurred in the past. In connection with the Venona project, American intelligence services intercepted encrypted Soviet communications sent during the Second World War. The code was cracked in 1946, and they later succeeded in gradually decrypting the messages, which notably revealed the extent of atomic espionage in favour of the USSR during the Manhattan Project.
So how can cryptography be made more robust in the face of quantum computers?
B. W.: By replacing vulnerable problems, such as the discrete logarithm, with more difficult ones that resist quantum algorithms. To do so, we must identify candidate problems and test their difficulty. This is where algorithmic cryptology plays a fundamental role, for it develops the best algorithms for solving these conundrums and testing their limits. By studying these techniques, we can adapt cryptography methods to make them more resistant to potential attacks. This algorithmic approach applies in general, not just as part of a post-quantum perspective. For decades, algorithmic cryptology has focused on classical problems such as the discrete logarithm. Today, collective efforts are largely redirected towards post-quantum quandaries.
Such as?
B. W.: There are a number of candidates, some revolving around cryptographic lattices. A cryptographic lattice is a regular arrangement of points in space, such as the intersection points on a mesh. One of the problems being studied is the following: within a given mesh, what are the two closest points that are possible? For a square mesh in 2D, the answer is easy to find. But if the mesh is not very simple, with a dimension of 100, 200, or 500, the task is much more complex, even for a quantum computer. Or at least we hope so, and we are continuing to put this possibility to the test.
Another candidate is based on elliptic curves and isogenies. This involves mathematical concepts that are fairly abstract, and are therefore more difficult to explain in a few words. Quite simply, in some cases, two elliptic curves can be connected by an ‘isogeny’, a formula allowing to go from one to the other. The problem, which is believed to be tricky, is the following: is it possible to find the isogeny connecting two given curves? These are the two problems I’m currently focusing on.
Further reading on our site
Towards a post-quantum cryptography
- 1. Pure and Applied Mathematics Unit (UMPA – CNRS / ENS Lyon).