You are here
Claire Voisin, Forms and Formulas
A specialist in algebraic geometry, a CNRS senior researcher at the IMJ1 until last June and now a professor at the Collège de France, 54-year-old Claire Voisin loves to philosophize about her profession. In fact, philosophy was her favorite subject at secondary school. At the time, she also felt drawn to poetry. Mathematics didn’t seem to hold much interest for her at first, but that would soon change…
Encouraged by her father, an alumnus of France’s prestigious École Polytechnique, Voisin began exploring the myriad implications of the basic theorems of plane geometry (Thales, Pythagoras…) and, from the age of 15, devoured all the specialized books that were “lying around the house.” When her father suddenly lost his job, she was granted a state scholarship to pursue her studies. After two years of preparatory classes, during which she developed a real taste for mathematics, she was admitted to the Ecole Normale Supérieure in 1981, at the age of 19. “I was paid a salary—it was great!” she recalls. “To me, it meant: ‘we’re happy that you’re studying, make the most of it!’”
Reconciling algebra and geometry
After earning a postgraduate teaching diploma in mathematics in 1983, she completed her dissertation three years later under the supervision of Arnaud Beauville. Immediately upon graduation, she was recruited by the CNRS and began what would prove to be a brilliant career. She won numerous prestigious awards, including a European Mathematical Society prize in 1992, and was elected to the Académie des Sciences in 2010. In 2016 she received the 2016 CNRS Gold Medal, France's highest scientific distinction, a few months after becoming the first female mathematician to join the Collège de France, where she holds the chair in algebraic geometry.
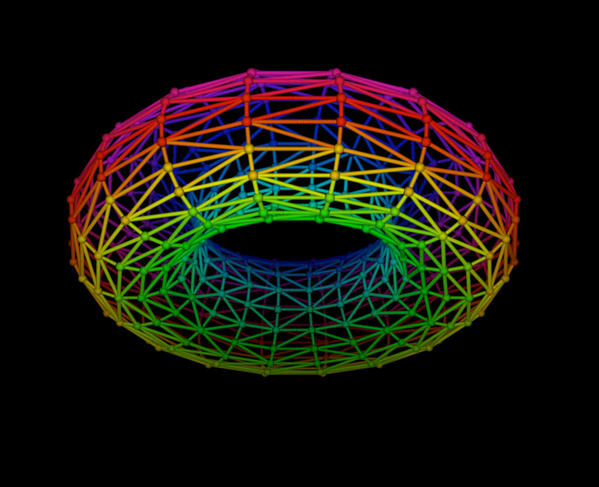
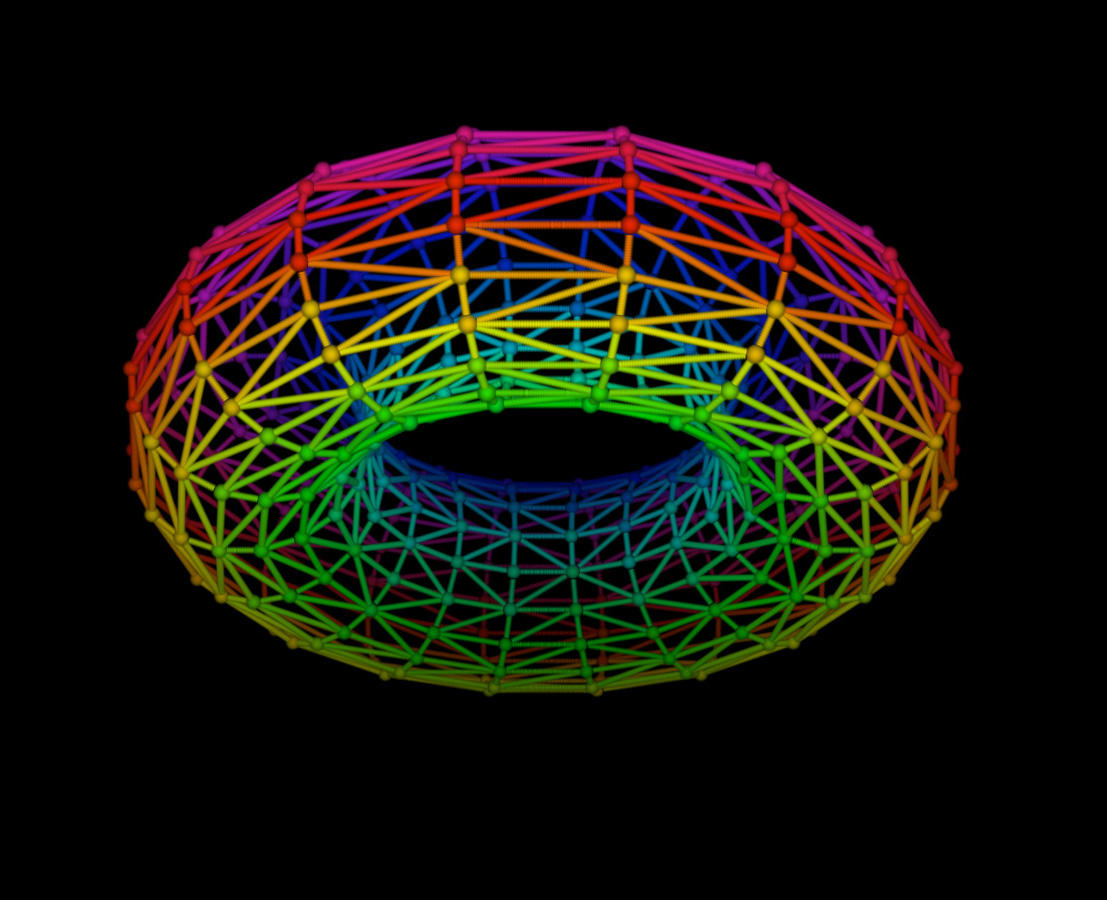
Confronted with our difficulty to understand what this high-flying discipline actually entails, she walks to the blackboard and draws a large torus framed by x- and y-axes. “At first sight, all we see here is a thick ring, like a lifebuoy, with one or several holes in the middle," she explains. But in mathematics, we seek to find out more: how do the curves plotted out on this torus intersect? What families of curves can cover the torus? Can the torus be unfolded and superimposed on a sphere? These are topological questions that can be dealt with using the Morse theory or Hodge theory, for example. These objects are also defined by complex algebraic equations, which offers different ways of approaching them.”
“What’s interesting in algebraic geometry is that you can do geometry to understand algebraic equations and algebra to elucidate geometric figures," adds François Charles, a professor at the Université Paris-Sud in Orsay (Paris) and one of Claire Voisin's former PhD students. There is a constant back and forth between the two approaches. But it also raises a problem: even though algebra and geometry are useful, each in its own way, to understand an object, we cannot always reconcile the two and find the link between them.” We are somewhat in the same situation as physicists, who are unable to unite all four fundamental interactions (forces of the Universe) in a single theory. Each one characterizes it in a different way, whether it be gravity, or electromagnetism, weak nuclear force and strong nuclear force.
A creative approach
Unlocking the mysteries of the Universe is an appealing prospect for nearly everyone. But what is the point of dissecting a torus or a sphere in mathematical terms? To this deliberately provocative question, Voisin responds with a heartfelt eulogy that reveals her passion for her chosen field: “It was mathematicians who, in ancient times, set out to calculate the radius of the Earth! Without mathematics, none of the progress in physics would have been possible. We need mathematics to study the structure of the Universe! All of the powerful theoretical tools we develop will find applications sooner or later.”
One of Voisin’s most outstanding findings concerns the Kodaira theorem on surfaces; she has proved that in higher dimensions some compact Kähler manifolds cannot be deformed to complex projective manifolds. She has also proved the impossibility of extending the Hodge conjecture to the Kählerian framework. In projective geometry, she has established Green’s conjecture for generic curves, based on a novel construction and complex calculations. Her current research on birational invariants has attracted a great deal of attention and was discussed on November 5, 2015 at the Nicolas Bourbaki seminar, a not-to-be-missed contemporary mathematics event.
”I don’t consider myself an artist, but it is true that you must be creative to achieve good results in mathematics. Actually, I painted a lot until the age of 25,” she divulges, pointing to the canvases hanging in her living room. “I stopped eventually—my profession calls upon most of one’s creative abilities.” When she was younger, she would immediately try and solve any intriguing mathematical problem that she came across. Yet this is not always possible today: Voisin has multiple responsibilities in relation to her colleagues and students, as well as... five children and a granddaughter. Her days can be hectic, so she now jots down her ideas in a small notebook—which she extricates from a pile of documents sitting on the floor—for further thought whenever she has time to herself.

“We have some remarkable institutions that help build the reputation of French mathematics around the world,” she concludes. “In schools however, it is an elite discipline, which tends to encourage arrogance. It is also unfortunate that students are only taught a combination of definitions, properties and theorems that make the subject seem rigid. Rather than ready-made mathematics, I would be in favor of a more open educational approach that gives pride of place to discovery and encourages students to ask more questions.”
- 1. Institut de Mathématiques de Jussieu (CNRS / UPMC / Université Paris Diderot).