You are here
Pretzels, Bagels, Doughnuts… and Topology
On October 4 and 5, 2016, representatives of the media were bombarded with pretzels, bagels and doughnuts, which the Nobel Committee was using to explain the work of three of its laureates, the physicists David J. Thouless, F. Duncan Haldane and J. Michael Kosterlitz. The researchers, whose results were described as highly mathematical, and therefore somewhat abstruse, were being honored for “theoretical findings in topological phase transitions.” According to the Committee, “Their discoveries have brought about breakthroughs in the theoretical understanding of matter's mysteries and opened up new perspectives on the development of innovative materials.” But what is the connection with bagels? And what exactly does topology do?
Heating water to 100°C to elucidate “phase transition"
All types of matter undergo phase transition when subjected to significant changes in temperature and pressure. For example, water turns into ice at 0°C and boils into steam at 100°C. The various phases (liquid, gas, solid) are characterized by very different organizations of the same molecules at the microscopic scale. In a solid, the atoms are highly organized and arranged in a near perfect periodic network. Knowing the position of a few atoms is enough to infer the position of the others with fairly high precision. The atoms are said to have long-range correlation. Inversely, the atoms in a gas are in constant and unpredictable motion, making it impossible to use the positions of a few to determine those of the others. As the temperature gradually changes, it reaches specific values (0°C and 100°C for water under normal conditions of pressure) at which the system passes abruptly from one phase to another.

Although we live in a three-dimensional world, the theories of Thouless, Haldane and Kosterlitz, the three laureate physicists, are based on fictional realms of only one or two dimensions: it is possible to stretch or flatten out certain physical systems to such an extreme that they are essentially linear or planar, and therefore behave as if in dimension one or two. But what happens when water is transformed into ice in a one- or two-dimensional world? In 1950, Léon Van Hove provided a response in a theorem that was generalized by David Mermin and Herbert Wagner in 1966—and finally extended to more general systems by multiple authors. This research concluded that, even at very low temperatures, one- or two-dimensional physical systems can never display long-range correlation (the Mermin-Wagner theorem). In other words, our world would be so different in dimensions one or two that water would never turn into ice.
As it happens, digital simulations in the early 1970s seemed to indicate the presence of a phase transition for various two-dimensional systems, contradicting the theorem. In 1973, David J. Thouless and J. Michael Kosterlitz finally understood what happened in two dimensions, which eventually earned them a Nobel Prize last year. The Soviet physicist Vadim Berezinskii had made similar but less advanced discoveries in 1970, which is why these findings are known as “BKT transition,” for Berezinskii-Kosterlitz-Thouless. The Soviet scientist would have shared the honor of last year’s Nobel, had he not died prematurely in 1980. The third laureate of 2016, F. Duncan Haldane, studied one-dimensional systems, leading to further breakthroughs in the topological properties of small materials.
Doughnuts, bagels and pretzels as practical examples
What exactly is the “BKT transition”? Kosterlitz and Thouless have postulated that small eddies can form in a two-dimensional fluid. Each eddy has a center around which the fluid rotates either clockwise or anticlockwise. A particle in the fluid near the eddy essentially follows a path that winds around the center. The study of these paths shows connections with certain mathematical concepts in topology—and pretzels, doughnuts and bagels are useful for understanding the phenomenon.
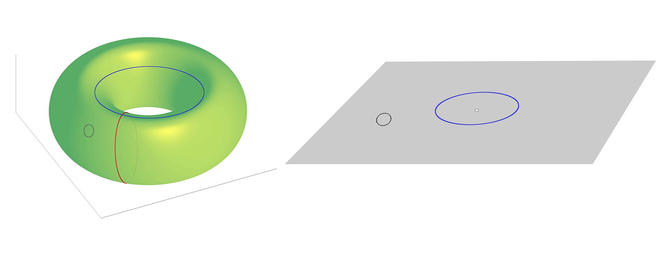
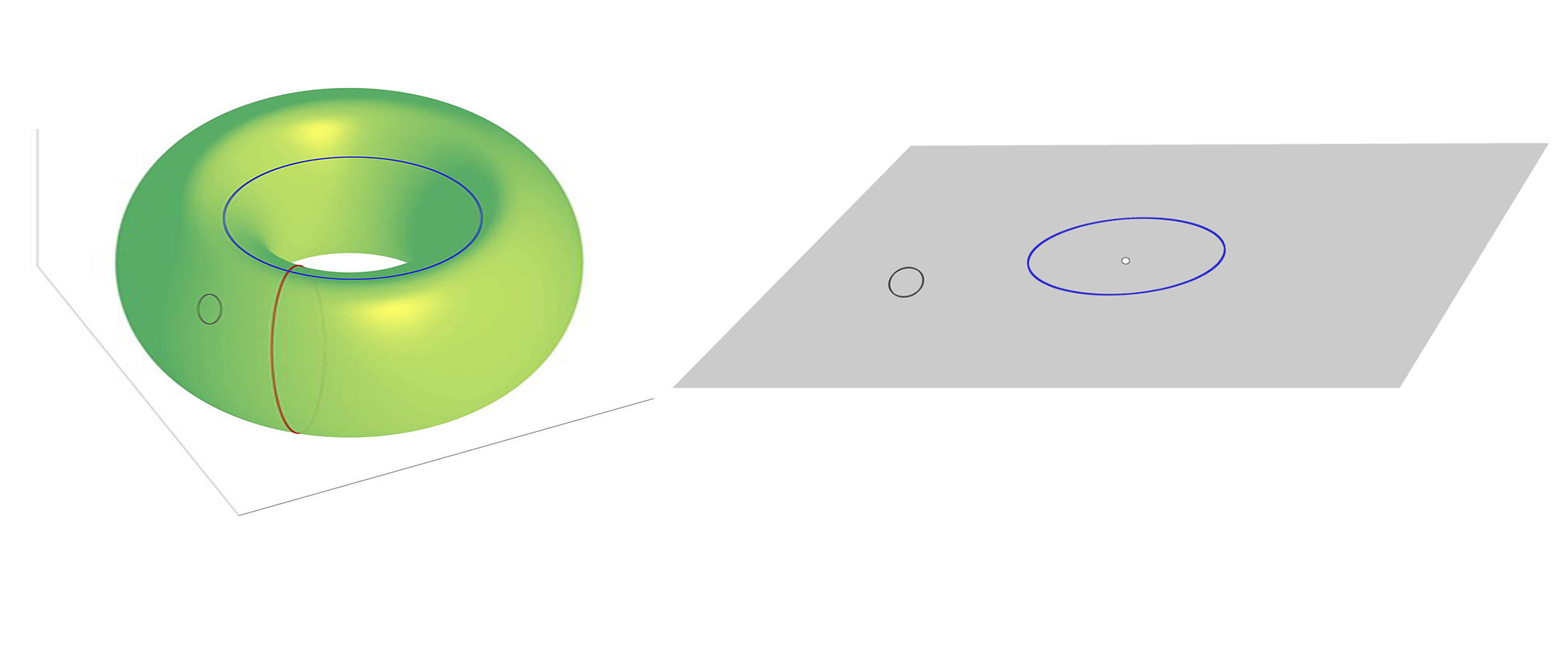
The mathematical theory in question consists in studying how loops can be deformed, contracted and moved on surfaces. A rubber band wrapped around a sphere, for example, can be gradually deformed without being lifted off the sphere and contracted on a single given point anywhere on the sphere. Now take a torus, a sort of “inner tube” shaped like a bagel or doughnut. Since it has a hole, there are various non-identical ways to place an elastic band on it. A small rubber band simply put on the surface of the torus can be deformed in the same way as on the sphere, but one that is wrapped around the torus can never be contracted on a single point. In fact, it can be wrapped around the body of the tube like a ring around a finger or placed around the periphery of the tube (the red and blue lines, respectively, in the figure below). These two new situations are not equivalent: it is impossible to move from one to the other by deforming the elastic. And of course, the classification of all the possible positions of rubber bands is even more complex for a pretzel, which has several holes.
The eddies studied by the physicists are actually a bit simpler than doughnuts, bagels and pretzels. Take a plane surface with a hole in it, however small. A rubber band placed far from the hole can be moved and contracted to an arbitrary point on the plane, but a band coiled around the hole can be contracted to that point only, to the exclusion of any other. However, when introducing the third dimension, in other words the possibility of taking the rubber band out of that single plane, the phenomenon disappears completely and all ways of placing the elastic become identical again. Therefore, from a topological point of view, making a hole in a plane is not at all the same thing as making a hole in a three-dimensional space. This is one of the mathematical reasons why physical systems behave very differently in two dimensions.
While Kosterlitz and Thouless already used the expression “topological phase transition” in their first article published in 1973, topology is actually only indirectly related to their work. The above-mentioned hole corresponds to the center of the eddy and the rubber bands, to the paths taken by the particles of fluid around it. Yet the physicists’ arguments do not use the formalism of topology directly. On the other hand, their work points the way toward a new mode of thinking that has led to models involving topology at a much more fundamental level.
Eddies and phase transitions
Back to Thouless and Kosterlitz’s eddies. In 1973, the two researchers had the insight that at low temperatures, the properties of fluids in two dimensions could be explained by eddies. In the first approximation, eddies attract and repel each other according to a universal law, independent of the fluid in question and identical to the law describing the movement of charged particles on a plane surface. Two eddies rotating in the same direction repel each other like two particles with the same charge. Two eddies rotating in opposite directions are attracted to each other and can cancel each other out.
In order to understand the role of eddies, Kosterlitz and Thouless simply replaced them with positively and negatively charged particles, forming a so-called Coulomb gas, or two-component plasma. They then demonstrated that an unusual type of phase transition occurs in such a simplified system. At a certain temperature, which can be precisely calculated, the positively charged particles suddenly pair off with the negative ones, and the number of pairs increases as the temperature drops. This is a new type of phase transition because it is not abrupt, like liquid water turning to ice in the freezer. The changes are gradual and more difficult to detect. The charged particles are not organized in a network, as they are in a three-dimensional solid. Instead, they form inseparable but free pairs, which results in a very weak kind of order on the microscopic scale.
What lies ahead
The BKT transition is an important source of intriguing and difficult mathematical problems. In a famous article published in 1981, Jürg Fröhlich and Thomas Spencer succeeded in demonstrating the existence of such a transition for a Coulomb gas and other systems of the same type, thus confirming Thouless and Kosterlitz’s predictions. To reach their conclusion, Fröhlich and Spencer had to invent a new mathematical method called “multiscale analysis,” which has subsequently been used in many other situations, some bearing no relation to phase transitions.
Unfortunately, researchers have not yet been able to prove that the transition in a Coulomb gas does indeed take place at the temperature predicted by Kosterlitz and Thouless. Nor have they determined a precise description of the behavior of a fluid of any type in which eddies appear. The attribution of the Nobel Prize in Physics should stimulate mathematicians’ interest in these fundamental questions.
The analysis, views and opinions expressed in this section are those of the authors and do not necessarily reflect the position or policies of the CNRS.