In physics as in everyday life, measuring comes down to determining the relation between two quantities of the same nature, of which one—supposedly constant—serves as a standard or unit. For a long time, the human body provided practical and readily available standards for measuring the distance between two objects by using feet, thumbs, or cubits. The issue with this type of standard is that while everyone has a foot, not everyone has the same shoe size. To make measures trustworthy and comparable, as well as to facilitate trade, a minimum amount of consistency must be ensured. In the end, standards for length based on an unvarying foot were adopted—based in France on the foot of the king—and known and recognized by most people. The major flaw of this system was that the standard foot was not the same depending on the country, region, or even period: the Roman foot was shorter than the English foot, which was itself smaller than the French pied du roi. This was true for units of weight and volume as well, which were also based on anthropomorphic standards, such as the pound or the handful. With the rise of the sciences and international trade, the need for more precise and universal units was increasingly felt throughout the century of the Enlightenment.

From the royal system to quantum mechanics

The French revolutionaries, who included numerous scientists, and who had just decapitated King Louis XVI, quickly abolished the pied du roi. The nearly 800 units in use at the time on French territory were replaced by an entirely new system of decimal units: meter, kilogram, and second. These no longer referred to anthropomorphic standards, but for the first time to precisely measured astronomical values that were considered at the time as being constant, natural, and universal, such as the duration of a day on Earth, or the length of a meridian. Since then, the metric system has undergone multiple evolutions and redefinitions, although it was always based, even indirectly, on physical constants. “A system of units is a human construction, and the definitions of the SI were therefore originally based on classical physics. The successive changes of definition grew out of a desire to use more stable and fundamental measures, thereby accompanying the progress of physics,” explains Jean-Philippe Uzan, physicist at l’Institut d’astrophysique de Paris.1 It is therefore hardly surprising that the future revision of the SI gives prominence to constants from quantum mechanics and relativity.

Units born of constants

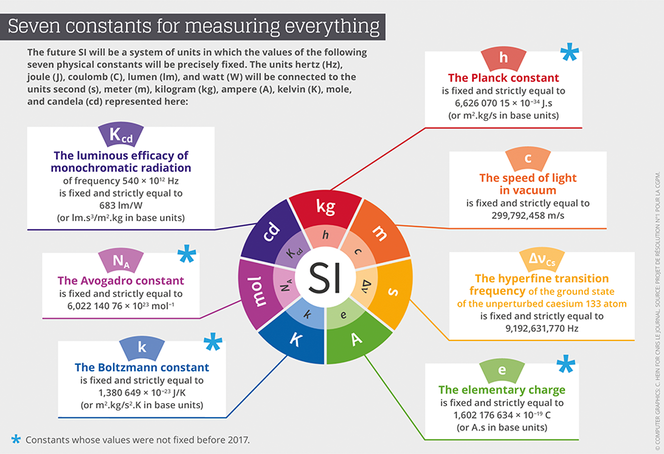
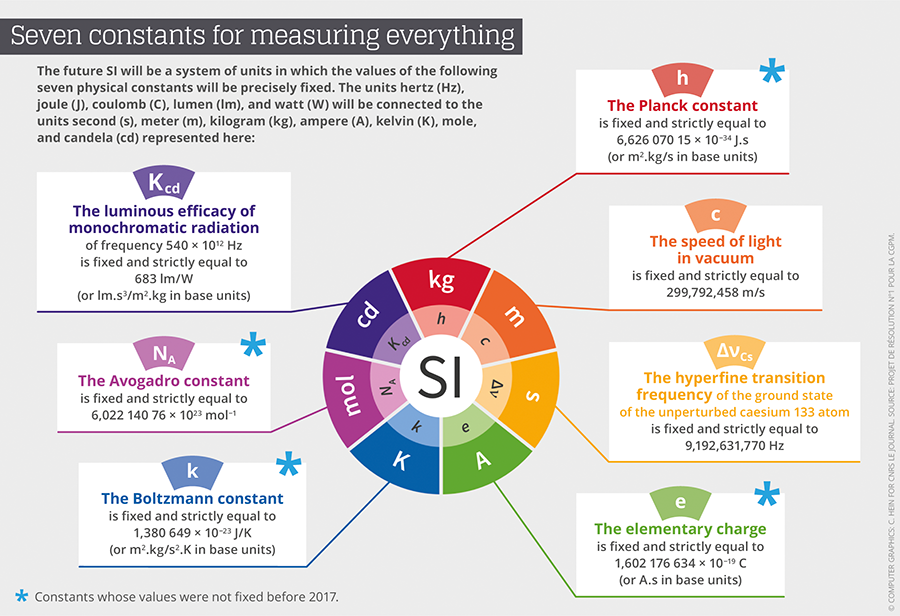
The redefinition of the seven base units will consequently be based on an explicit-constant formulation, which is a definition in which the unit is defined indirectly, and one that gives an exact value to a recognized fundamental constant. “We define as a fundamental constant of a theory of physics any parameter for which this theory can predict the value,” Uzan points out. This value can therefore not be obtained empirically through a measurement. Advances in instrumentation have already provided measures that are sufficiently precise to allow for conventionally establish exact values for some of them. Thus, after the value of c, the speed of light, was fixed in 1983, came the turn of h, the Planck constant, e, the electrical charge of the electron, k, the Boltzmann constant, and N_A, the Avogadro constant, to be etched in the SI’s tables. 

Seven constants for measuring everything.

Seven constants for measuring everything.

C. Hein pour CNRS le Journal. Sources: projet de résolution n°1 pour la CGPM Partager

C. Hein pour CNRS le Journal. Sources: projet de résolution n°1 pour la CGPM Partager

Share

Share

The CGPM has provided a very detailed roadmap on how the different fundamental constants involved in the new SI should be remeasured,2 before fixing their numerical values definitively. For instance for the Planck constant, the Conference demanded two independent methods, each applied in a number of metrology laboratories throughout the world. The first was based on the Kibble balance (also called a watt balance), which can balance masses with electromagnetic forces. The second consists of counting the atoms of a sphere of silicon 10 centimeters in diameter in order to define the Avogadro constant, and to then deduce a value of the Planck constant by using other known fundamental constants.

Realization of units

Once again, the discussions were tense. “The two methods did not yield exactly the same result. Some people subsequently wanted to push back the delivery date for the new system,” notes Christian Bordé. Yet “the different measures were all within the margin of error fixed by the Consultative Committee for Mass and Related Quantities,” explains François Nez. That is a way of saying that one ultimately has to make a decision.

Incidentally, it is a French team from the Laboratoire commun de métrologie LNE-Cnam that provided the value for the Boltzmann constant (k) with the smallest relative level of uncertainty, or 0.57x10^-6, inferior by a factor of three to the preceding state of the art. The value obtained by the French physicists will contribute 55% of k’s value, which will finally be set in stone. France is also contributing to the value of h through the Kibble balance of the Laboratoire national de métrologie et d’essais (LNE) in Trappes, and the measuring of other fundamental constants at the Kastler-Brossel Laboratory.

More specifically, these adjustments are the work of the Committee on Data for Science and Technology (CODATA),3 which since 1966 has been tasked with keeping the list and value of fundamental constants in physics up to date. “Our work consists of bringing about the synthesis of different measures deemed valid, in order to determine the fundamental constants. Their most likely values are obtained through a ‘least squares’ adjustment, based on all of the measures and physics relations that connect these constants. We can thus guarantee the coherence of the whole,” explains Nez, a member of CODATA. This coherence was deemed satisfactory by the CIPM in late 2017 during its 106th session, which duly noted that the conditions fixed to proceed with the revision of the SI had been met, opening the way for the adoption of the new system by the CGPM scheduled for November.

Incalculable values

“The numerical value of any constant completely depends on the chosen system of units,” Uzan reminds. For example, high-energy physicists sometimes use Planck units, for which the values of the constants h, c, and G are all fixed by convention at 1. This considerably simplifies the writing of equations that describe the laws of physics… but provides units that are not very practical as soon as we leave the realm of the infinitely small.

Constants and theories of physics

Constants and theories of physics

P. VAKHRUSHEV/AdobeStock.com

P. VAKHRUSHEV/AdobeStock.com

Share

Share

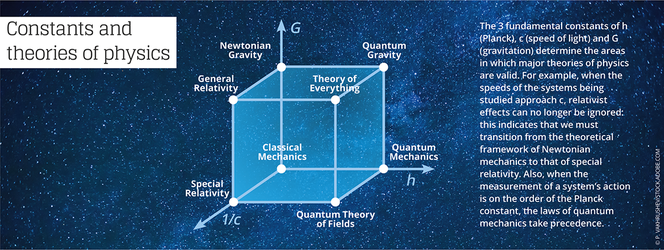
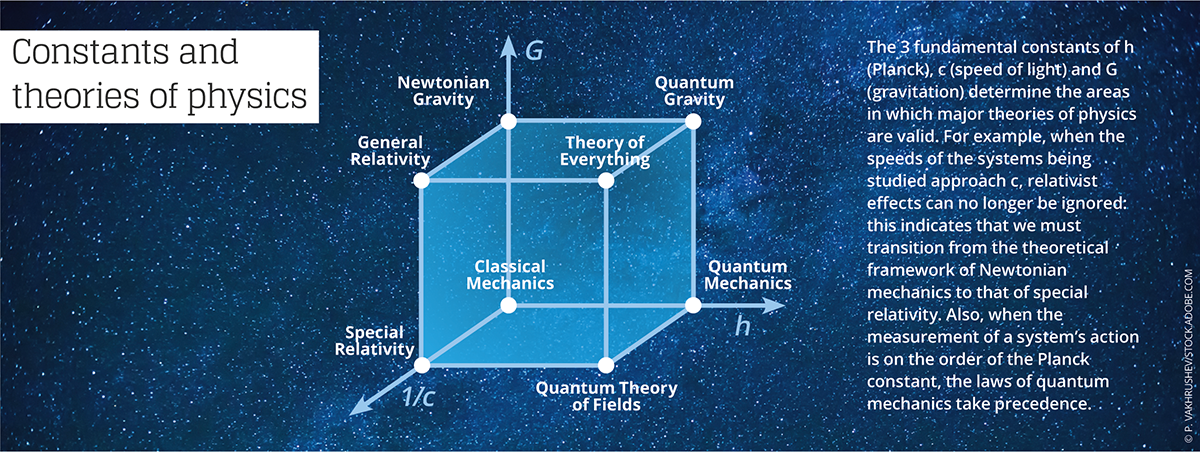
The physicist and epistemologist Jean-Marc Lévy-Leblond4 notes that “these universal constants not only play a role as a standard in the definition and measure of physical quantities, but are also used as norms of validity for theories in physics. This aspect is often summarized in assertions such as ‘Galilean relativity is obtained from Einsteinian relativity when the constant c tends toward infinity,’ or ‘quantum mechanics boils down to classical mechanics when the Planck constant tends toward zero.’”

The “exact” constants fixed by the SI are in fact no more than a subsection of the thirty or so that can be found in equations describing the laws of physics that govern our Universe: these range from the gravitational constant to masses of elementary particles and the coupling constants for the various forces of nature. These fundamental constants, which cannot be calculated, also emphasize the limits of our physical theories. “Most physicists are convinced that a future theory of fundamental particles will explain (or at least should explain) the diversity of their masses based on a few constants on a deep level, whether it be the masses of more elementary components, or a certain characteristic length,” observes Jean-Marc Lévy-Leblond. “When we have built this theory, these masses will be completely removed from the table of fundamental constants, and they will take on the status of derivative quantities.”

Synthesizing concepts

The number and status of constants that physicists use reflect the evolution of theories in physics, by making explicit the unit of certain physical phenomena. “By establishing bridges between quantities previously deemed incommensurable, constants make possible the emergence of new concepts,” remarks Uzan. “For example, c synthesizes space and time, the Planck constant h connects concepts of energy and frequency, and the gravitational constant G creates a link between matter and space-time.” This conceptual unification changes the status of the constants in question, and can even lead to abandoning certain sizes and units. “Joule’s discovery that heat and energy were two forms of energy resulted in the Joule constant, which expresses the proportionality between work and heat, losing all physical sense and becoming a simple factor of conversion between units measuring heat (calories) and work (joule). Today the calorie has become obsolete.”